Rectified 24-cell
| Rectified 24-cell | ||
 Schlegel diagram 8 of 24 cuboctahedral cells shown | ||
| Type | Uniform 4-polytope | |
| Schläfli symbols | r{3,4,3} = rr{3,3,4}= r{31,1,1} = | |
| Coxeter diagrams | ||
| Cells | 48 | 24 3.4.3.4 24 4.4.4 |
| Faces | 240 | 96 {3} 144 {4} |
| Edges | 288 | |
| Vertices | 96 | |
| Vertex figure |    Triangular prism | |
| Symmetry groups | F4 [3,4,3], order 1152 B4 [3,3,4], order 384 D4 [31,1,1], order 192 | |
| Properties | convex, edge-transitive | |
| Uniform index | 22 23 24 | |

In geometry, the rectified 24-cell or rectified icositetrachoron is a uniform 4-dimensional polytope (or uniform 4-polytope), which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by rectification of the 24-cell, reducing its octahedral cells to cubes and cuboctahedra.[1]
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC24.
It can also be considered a cantellated 16-cell with the lower symmetries B4 = [3,3,4]. B4 would lead to a bicoloring of the cuboctahedral cells into 8 and 16 each. It is also called a runcicantellated demitesseract in a D4 symmetry, giving 3 colors of cells, 8 for each.
Construction
[edit]The rectified 24-cell can be derived from the 24-cell by the process of rectification: the 24-cell is truncated at the midpoints. The vertices become cubes, while the octahedra become cuboctahedra.
Cartesian coordinates
[edit]A rectified 24-cell having an edge length of √2 has vertices given by all permutations and sign permutations of the following Cartesian coordinates:
- (0,1,1,2) [4!/2!×23 = 96 vertices]
The dual configuration with edge length 2 has all coordinate and sign permutations of:
- (0,2,2,2) [4×23 = 32 vertices]
- (1,1,1,3) [4×24 = 64 vertices]
Images
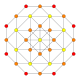
[edit]| Coxeter plane | F4 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | [12] | |
| Coxeter plane | B3 / A2 (a) | B3 / A2 (b) |
| Graph | 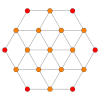
|
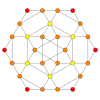
|
| Dihedral symmetry | [6] | [6] |
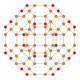
| Coxeter plane | B4 | B2 / A3 |
| Graph | 
|

|
| Dihedral symmetry | [8] | [4] |
| Stereographic projection | |
|---|---|
 | |
| Center of stereographic projection with 96 triangular faces blue | |
Symmetry constructions
[edit]There are three different symmetry constructions of this polytope. The lowest construction can be doubled into by adding a mirror that maps the bifurcating nodes onto each other. can be mapped up to symmetry by adding two mirror that map all three end nodes together.
The vertex figure is a triangular prism, containing two cubes and three cuboctahedra. The three symmetries can be seen with 3 colored cuboctahedra in the lowest construction, and two colors (1:2 ratio) in , and all identical cuboctahedra in .
| Coxeter group | = [3,4,3] | = [4,3,3] | = [3,31,1] |
|---|---|---|---|
| Order | 1152 | 384 | 192 |
| Full symmetry group |
[3,4,3] | [4,3,3] | <[3,31,1]> = [4,3,3] [3[31,1,1]] = [3,4,3] |
| Coxeter diagram | |||
| Facets | 3: 2: |
2,2: 2: |
1,1,1: 2: |
| Vertex figure | 
|

|

|
Alternate names
[edit]- Rectified 24-cell, Cantellated 16-cell (Norman Johnson)
- Rectified icositetrachoron (Acronym rico) (George Olshevsky, Jonathan Bowers)
- Cantellated hexadecachoron
- Disicositetrachoron
- Amboicositetrachoron (Neil Sloane & John Horton Conway)
Related polytopes
[edit]The convex hull of the rectified 24-cell and its dual (assuming that they are congruent) is a nonuniform polychoron composed of 192 cells: 48 cubes, 144 square antiprisms, and 192 vertices. Its vertex figure is a triangular bifrustum.
Related uniform polytopes
[edit]| D4 uniform polychora | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|

|
|

|

|

|
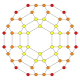
|
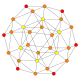
| ||||
| {3,31,1} h{4,3,3} |
2r{3,31,1} h3{4,3,3} |
t{3,31,1} h2{4,3,3} |
2t{3,31,1} h2,3{4,3,3} |
r{3,31,1} {31,1,1}={3,4,3} |
rr{3,31,1} r{31,1,1}=r{3,4,3} |
tr{3,31,1} t{31,1,1}=t{3,4,3} |
sr{3,31,1} s{31,1,1}=s{3,4,3} | ||||
| 24-cell family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | 24-cell | truncated 24-cell | snub 24-cell | rectified 24-cell | cantellated 24-cell | bitruncated 24-cell | cantitruncated 24-cell | runcinated 24-cell | runcitruncated 24-cell | omnitruncated 24-cell | |
| Schläfli symbol |
{3,4,3} | t0,1{3,4,3} t{3,4,3} |
s{3,4,3} | t1{3,4,3} r{3,4,3} |
t0,2{3,4,3} rr{3,4,3} |
t1,2{3,4,3} 2t{3,4,3} |
t0,1,2{3,4,3} tr{3,4,3} |
t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| Coxeter diagram |
|||||||||||
| Schlegel diagram |

|

|

|

|

|

|

|

|

|

| |
| F4 | 
|

|

|

|

|

|

|

|

|

| |
| B4 | 
|

|

|

|
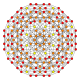
|

|

|

|

|

| |
| B3(a) | 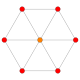
|

|

|

|

|

|

|

|
|

| |
| B3(b) | 
|

|

|
|

|
| |||||
| B2 | 
|

|

|

|

|

|

|
|
|

| |
The rectified 24-cell can also be derived as a cantellated 16-cell:
| B4 symmetry polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | tesseract | rectified tesseract |
truncated tesseract |
cantellated tesseract |
runcinated tesseract |
bitruncated tesseract |
cantitruncated tesseract |
runcitruncated tesseract |
omnitruncated tesseract | ||
| Coxeter diagram |
= |
= |
|||||||||
| Schläfli symbol |
{4,3,3} | t1{4,3,3} r{4,3,3} |
t0,1{4,3,3} t{4,3,3} |
t0,2{4,3,3} rr{4,3,3} |
t0,3{4,3,3} | t1,2{4,3,3} 2t{4,3,3} |
t0,1,2{4,3,3} tr{4,3,3} |
t0,1,3{4,3,3} | t0,1,2,3{4,3,3} | ||
| Schlegel diagram |

|

|
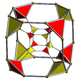
|

|

|

|
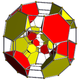
|
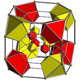
|

| ||
| B4 | 
|

|

|

|
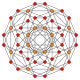
|

|

|
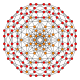
|

| ||
| Name | 16-cell | rectified 16-cell |
truncated 16-cell |
cantellated 16-cell |
runcinated 16-cell |
bitruncated 16-cell |
cantitruncated 16-cell |
runcitruncated 16-cell |
omnitruncated 16-cell | ||
| Coxeter diagram |
= |
= |
= |
= |
= |
= |
|||||
| Schläfli symbol |
{3,3,4} | t1{3,3,4} r{3,3,4} |
t0,1{3,3,4} t{3,3,4} |
t0,2{3,3,4} rr{3,3,4} |
t0,3{3,3,4} | t1,2{3,3,4} 2t{3,3,4} |
t0,1,2{3,3,4} tr{3,3,4} |
t0,1,3{3,3,4} | t0,1,2,3{3,3,4} | ||
| Schlegel diagram |
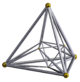
|

|

|

|

|
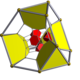
|

|
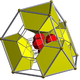
|

| ||
| B4 | 
|

|

|

|

|

|

|

|

| ||
Citations
[edit]- ^ Coxeter 1973, p. 154, §8.4.
References
[edit]- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 23, George Olshevsky.
- 3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 23, George Olshevsky.
- 7. Uniform polychora derived from glomeric tetrahedron B4 - Model 23, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) o3x4o3o - rico".






